はじめに
モーメントの定義について,初級レベルではなく,中級レベルでの理解を目指した解説をしたいと思います。
高校では物理をあまり学んでおらず,理学療法士養成校で運動学を習ってから,物理も勉強してみようと思い始めたぐらいの方が対象になります。
最後に国家試験問題もとりあげます。
モーメント(トルク)について簡単に
先ずは,理学療法士養成校で最低限必ず習うであろう内容をまとめます。
モーメント(トルク)とは,物体を回転させる強さのことです。
そして,モーメントの大きさはモーメントアームの長さと力の大きさの積です。
モーメント = モーメントアーム × 力
モーメントアームとは,回転軸から力が加わるところまでの距離です。
単位は Nm です(長さは m,力は N)。
スパナでボルトを締める場合,柄が長い方がよく締まります。
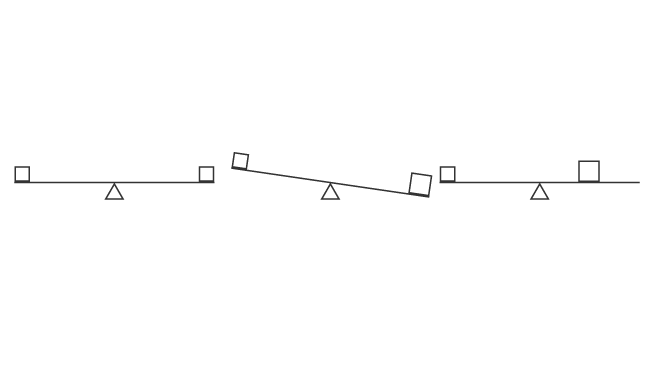
シーソーでは,重さが同じで,軸からの距離も同じであれば,モーメントが同じになって釣り合います(図 1 左)。
重さが異なり,軸からの距離は同じだと,重い方のモーメントが大きくなり,重い方が下がります(図 1 中央)。
重い方が軸に近づいてモーメントが小さくなり,軽い方のモーメントと同じになれば,そこで釣り合います(図 1 右)。
モーメントの正確な定義
物理学での正確なモーメントの定義式を示します。
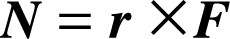
N はモーメント,r は力の作用点の位置ベクトル,F は力です。
全て太字になっています(太字だとは分かりにくくなっていますが,,,)。
物理学や数学では,太字はベクトルを意味します。
つまり,モーメントはベクトルで定義されますし,モーメント自体もベクトルです。
ベクトル同士の掛け算は,普通の掛け算ではなく,外積と呼ばれる計算になります(外積の計算方法については,理学療法の範疇ではなさそうですので省きます)。
外積によって得られたベクトルは,元のベクトルの両方に対して垂直です(図 2)。
また,右手の法則に従った向きになります(右手の法則についてはこちら)。
そして,外積の大きさは,元のベクトルが作る平行四辺形の面積に等しくなります(図 2)。
「モーメントアーム × 力」という計算は,四角形の面積を求めていることにほかなりません。
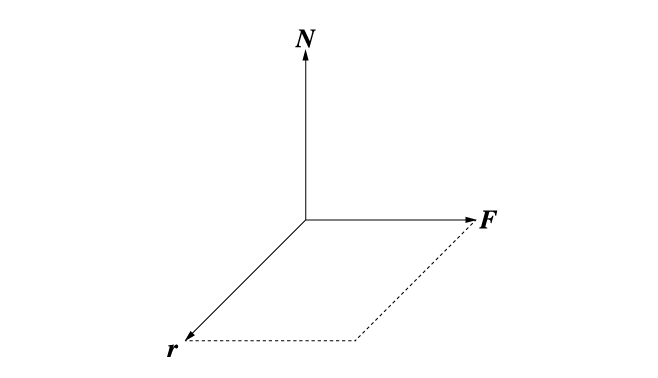
「モーメントアーム × 力」とすれば,ベクトルの外積などという難しい概念を使わずに,モーメントを理解することができます。
しかし,力の方向が斜めだと,三角比を使わなければなりませんし,条件によっては使えないこともありますので,定義式としては不十分です。
国家試験問題
古い国家試験問題です。
物理学での正式な定義を使うと解けなくなる問題です。
第 48 回理学療法士国家試験 午前 69
同一平面内に働く力ベクトル F1 と F2 が同じ平面上の点 O の回りに作るモーメント M を表す式はどれか。
ただし,O からベクトル F1 と F2 の作用線に下ろした垂線の長さをそれぞれ a,b とする。
1.M = F1 + F2
2.M = aF1 + bF2
3.M = (aF1 + bF2) / 2
4.M = (F1 + F2) / (a + b)
5.M = (F1 + F2)(a + b)
正解 2
この問題は,モーメントについて問う物理学の問題になっています。
抽象的な問題であり,膝関節伸展に抵抗をかけたときのモーメントなどといった具体的な場面に関する問題ではありません。
問題の設定は「同一平面内に働く力ベクトル F1 と F2 が同じ平面上の点 O の回りに作るモーメント」です。
ちょっと難しい表現ですね。
これは,例えば,ハンドルを両手で回す場面だと思えばいいと思います。
F1は左手,F2は右手といったところです。
ハンドルの中心とハンドルを持っているところは同じ平面上であり,力をかける方向はハンドルを傾けるような方向ではないということです。
2 次元で考えればいいということでもあります。
次に,a と b についてです。
力の方向がモーメントアームに対して垂直でない場合は,力のベクトルを分解し,力の強さを三角比を使って計算しなければなりません。
分解すれば力は小さくなり,モーメントも小さくなります。
この問題では,力とモーメントアームの角度が提示されておらず,力のベクトルを分解することができません。
代わりに,O からベクトル F1 と F2 の作用線に下ろした垂線の長さである,a と b が提示されています。
a と b はモーメントアームの代わりになります。
力が小さくなる代わりにモーメントアームが短くなるということです。
この方法が正しいことの証明は省きます。
この問題が,「モーメントの大きさを表す式はどれか」という問題であれば,選択肢 2 がほぼ正解です。
F1 と F2 のそれぞれでモーメントアームに力をかけて,合計する式になっています。
しかし,F1 と F2 はベクトルであり,力の大きさを表す数値ではありません。
ですので,それにモーメントアームの長さをかけても,モーメントの大きさは分かりません。
F1 と F2 がベクトルではなく,ベクトルの大きさを表しているのだと解釈したとすれば,選択肢 2 の式はモーメントの大きさを表しますが,それでも正解にはなりません。
力の方向が正反対の場合はどうなるでしょう。
ハンドルを両手で回す場合,左手は左に,右手は右に,同じ強さで回そうとすればハンドルは回りません。
このとき,モーメントの大きさは 0 にならないといけないのですが,選択肢 2 の式では,正の数字になってしまいます。
具体的な場面に関する問題ではないため,どんな場合でも成り立つ式でなければなりません。
問題文の通りであれば,モーメントを求めることはできません。
モーメントは,力の作用点の位置ベクトルと力のベクトルの外積です。
問題の設定では,力の作用点の位置ベクトルが分からないため,モーメントを計算することはできません。
もしかしたら,力の作用点の位置ベクトルを算出する方法があるのかもしれませんが,私には分かりませんし,少なくとも選択肢 2 の式には,力の作用点の位置ベクトルは含まれていないと思います。
以上のことから,この問題は不適切問題になると思いますが,モーメントについてちょっと深く学ぶことができるという点ではいい問題だと思います。
おわりに
モーメントの物理学での正確な定義を知らなくても,モーメントアームが長ければ回転する力は強くなるということさえ知っていれば,臨床では特に困ることはありません。
今回取り上げた国家試験問題では,モーメントの正確な定義を知らない方が,悩むことなく解答することができるのかもしれません。
しかし,このような問題が出題されることは,業界全体の信頼に関わることです。
やはり,基本的なところはちゃんと理解しておく方が望ましいと思います。
あわせて読みたい
スポンサーリンク参考文献
1)P. D. Andrew, 有馬慶美, 日髙正巳(監訳):筋骨格系のキネシオロジー 原著第3版. 医歯薬出版, 2020, pp16-17.
2)兵頭俊夫: 運動と力. 放送大学教育振興会, 2005, pp96-105.
3)桑村雅隆: リメディアル線形代数-2次元行列と図形からの導入. 裳華房, 2007, pp49-54.
2021年8月26日


コメント