はじめに
運動学などでは,三次元の座標軸を決めるとき,右手の法則を使います。
右手の法則について解説します。
右手の法則についてまず覚えておきたいところ
右手の法則とは,x 軸,y 軸,z 軸をどちら向きにするかを決める法則です。
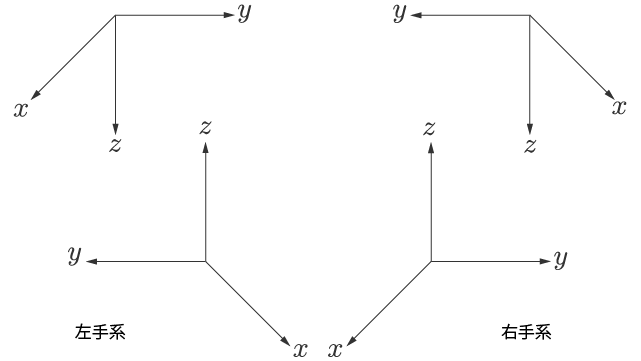
右手の法則に従った座標軸を図 1 に示します。
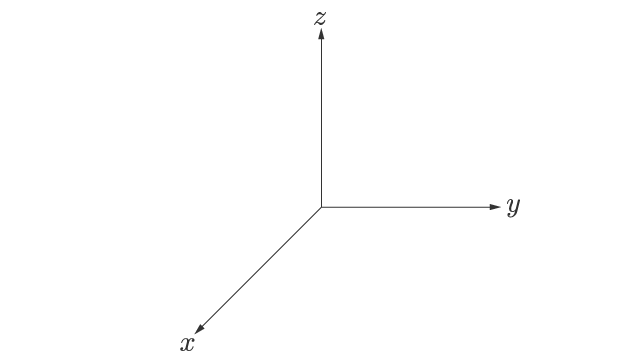
右手の法則の意味が分かっていなくても,図 1 のような座標軸を書くことができれば,運動学の教科書なども理解しやすくなると思います。
ですが,ちゃんと意味を理解していれば,より理解は深まります。
右手の法則を理解するためには,図 1 の座標軸とは異なる座標軸があることを理解する必要があります。
右手があるなら左手もあるはずですよね。
右手系と左手系の区別
座標軸には 右手系と左手系の 2 種類があります。
図 1 は右手の法則に従った右手系の座標軸ですが,それとは逆向きの座標軸があるということです。
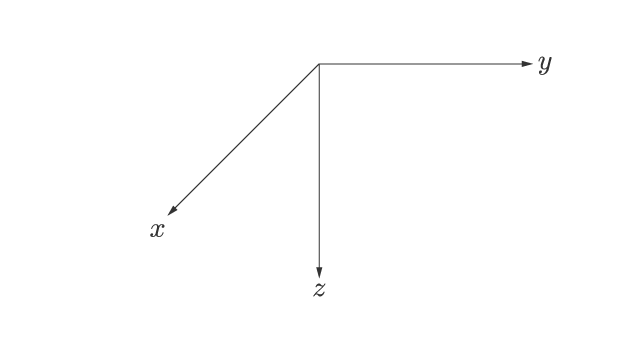
z 軸を逆にするのが分かりやすいと思います。
図 2 に示します。
右手系と左手系を並べてみます(図 3)。
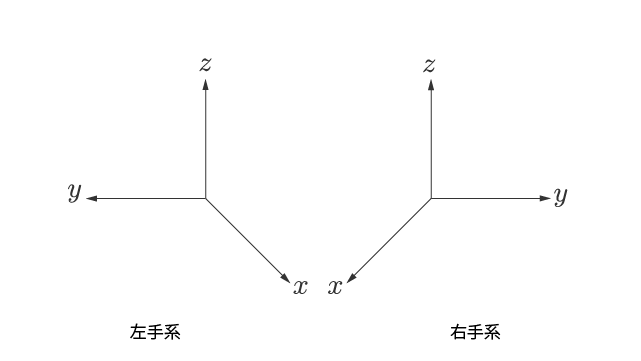
左手系は図 2 で示したものの上下をひっくり返しています。
右手系と左手系が異なるものであることをしっかり確認してください。
二つの座標軸は移動したり回転したりしても重ね合わせることはできません。
x 軸どうしと y 軸どうしを重ねると,z 軸は重なりません。
ですので,右手系と左手系は区別されます。
右手系と左手系は鏡に映したような関係になっているところも注目ポイントです。
どこが右手なのか
右手の親指,人差し指,中指を互いに直交するように伸ばします。
右手の親指を x 軸,人差し指を y 軸,中指を z 軸とすると,右手系の座標軸になります。
同じことを左手ですると,逆向きの左手系の座標軸になります。
右手と左手はどうやっても重なりません。
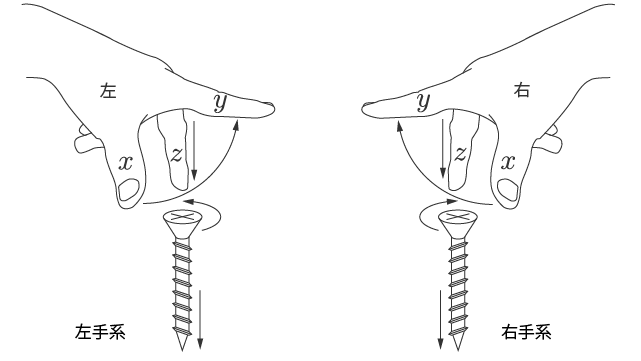
右ねじの法則とも呼ぼれます。
右ねじは,ねじの頭からみて右に回すとねじ込まれます。
親指から人差し指に向かって回転させると中指の方向に進むねじです。
左ねじは逆になります。
図 4,5 に示します。
おわりに
右手系と左手系のどちらを使うのかは分野によって異なりますが,右手系が使われることが多いようです。
文献を読むときには,左右を間違えないことが肝心です。
実際のねじも右ねじが主流です。
その理由は,前腕の筋力は回内筋群よりも回外筋群の方が強いからであり,右手の回外によってねじを締めるためです3)。
力のモーメントは右手系で表現されます。
モーメントの定義については以下の記事でまとめています。
参考文献
1)桑村雅隆: リメディアル線形代数-2次元行列と図形からの導入. 裳華房, 2007, pp49-54.
2)長岡亮介: 線形代数入門. 放送大学教育振興会, 2003, pp9-20.
3)P. D. Andrew, 有馬慶美, 日髙正巳(監訳):筋骨格系のキネシオロジー 原著第3版. 医歯薬出版, 2020, pp99-231.
2021 年 9 月 11 日
2021 年 11 月 4 日
コメント