はじめに
筋骨格系のてこにおける力学的有利性の定義と意味について解説します。
目次
てこの定義
てことは,棒を一つの点(軸)で支え,その点を中心として回転できるようにしたものです。
力や移動距離を増幅することができます。
てこには支点,力点,作用点があります。
支点はてこを支える点です。
筋骨格系のてこでは,主には関節が支点になります。
力点は力を加える点です。
筋骨格系のてこでは,筋の張力(内力)が作用する点に相当します。
作用点(荷重点)は,力点に加えられた力がてこを介して作用する点,あるいは荷重による力がかかる点のことです。
筋骨格系のてこでは,外力の作用する点であり,筋が動かそうとするものの重心に相当します。
てこの種類
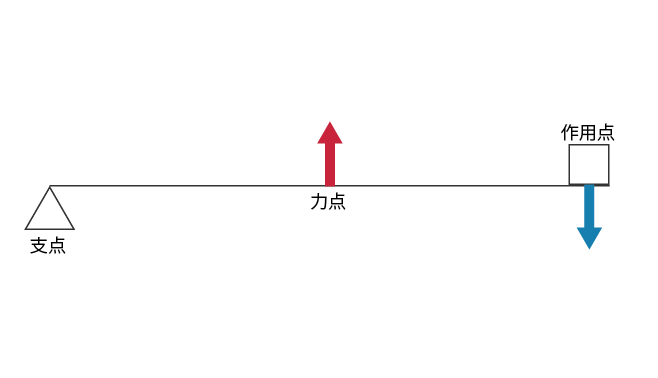
てこは,支点,力点,作用点の位置関係によって,3 つに分類されます。
第 1 のてこ
支点が力点と作用点の間にあるてこです(図 1)。
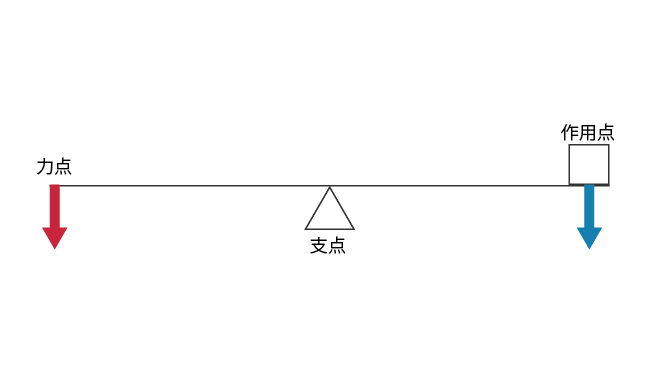
人体での第 1 のてこの例として,頭部前後屈の頭部伸筋群による制御があります(図 2)。
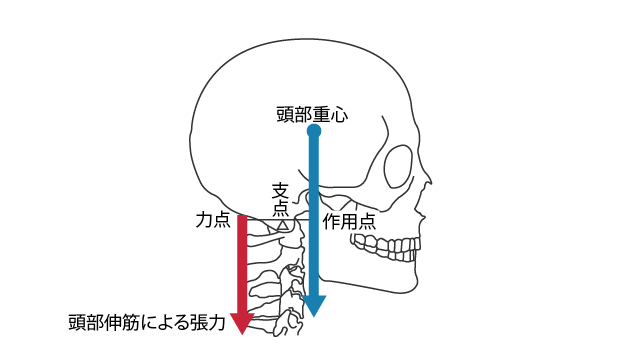
上腕三頭筋による肘伸展や片脚立位での中殿筋による骨盤の安定化も第 1 のてこです。
第 2 のてこ
作用点が支点と力点の間にあるてこです(図 3)。
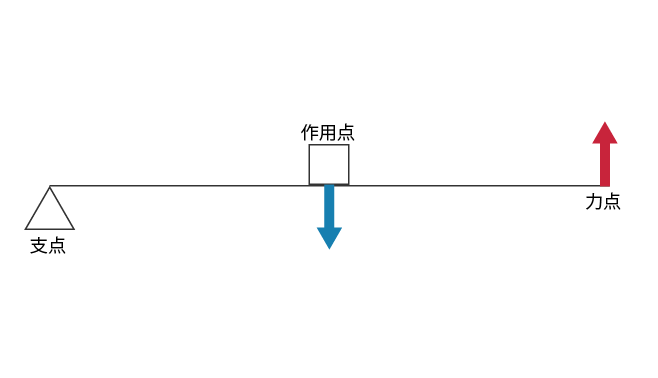
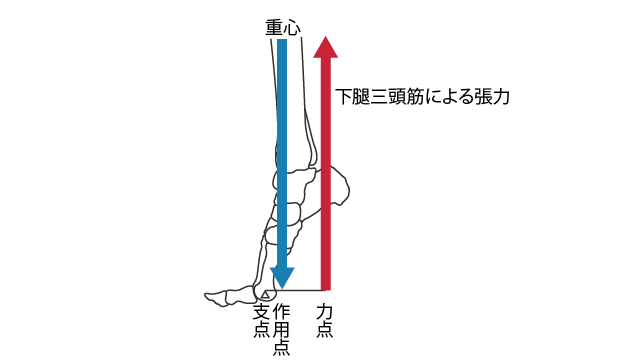
人体での例としては,つま先立ちでの下腿三頭筋の活動があります(図 4)。
腕橈骨筋による肘関節屈曲や開口も第 2 のてこです。
下腿三頭筋の例は,支点は距腿関節,作用点は中足骨頭として,第 1 のてこであると解釈することも可能かもしれません。
第 3 のてこ
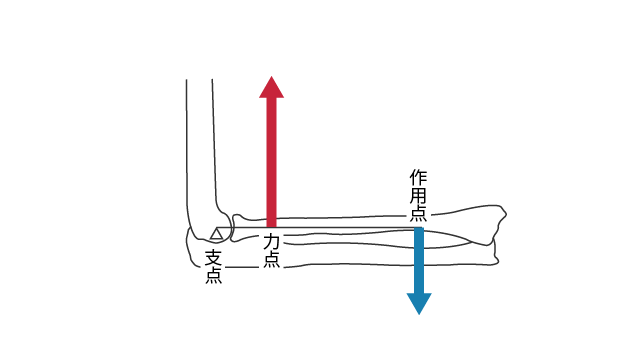
力点が支点と作用点の間にあるてこです(図 5)。
人体での例としては,肘関節屈曲位を抗重力位で保持するときの肘関節屈筋の活動があります。
力学的有利性の定義
筋骨格系のてこにおける力学的有利性(mechanical advantage MA)とは,内的モーメントアームと外的モーメントアームの比のことです。
力学的有利性 = 内的モーメントアーム / 外的モーメントアーム
内的モーメントアームとは,てこの支点から力点までの距離のことです。
外的モーメントアームとは,てこの支点から荷重点までの距離のことです。
力学的有利性の意味
モーメント = モーメントアーム × 力ですので,モーメントアームが長くなれば,モーメントは大きくなります。
つまり,モーメントアームが長ければ,同じ力でもより大きな回転力を生むことができ,回転力を生むとという点で有利であるということです。
力学的有利性 > 1
内的モーメントアームの方が長ければ,力学的有利性は 1 より大きくなります。
筋が生み出す張力が外力より小さくても釣り合いを保つ(外力に抗して静止する)ことができます。
力学的有利性 > 1 の場合を力学的に有利な系といいます2)。
第 2 のてこでは,力学的有利性は必ず 1 より大きくなります。
第 2 のてこは,力を増幅するてこであるといえます。
力学的有利性 < 1
内的モーメントアームの方が短ければ,力学的有利性は 1 より小さくなります。
釣り合いを保つためには,筋は外力よりも大きな張力を生み出す必要があります。
第 3 のてこでは,力学的有利性は必ず 1 より小さくなります。
第 3 のてこは,力を増幅することはできませんが,移動距離や速さは増幅することができます。
人体では第 3 のてこが多く,力学的有利性でみれば不利な構造ですが,移動距離や速さにとっては有利な構造になっています。
力学的有利性 = 1
内的モーメントアームと外的モーメントアームの長さが同じであれば,力学的有利性は 1 です。
釣り合いを保つには,筋は外力と同じだけの張力を発揮すれば済みます。
力学的有利性が 1 になりうるのは通常は第 1 のてこだけですが,第 1 のてこでは,支点の位置によって,力学的有利性は 1 より大きくなったり,小さくなったりします。
おわりに
てこに関する知識は,運動を分析する際に必要になりますので,確実に覚えておきたいところです。
あわせて読みたい
参考文献
1)P. D. Andrew, 有馬慶美, 日髙正巳(監訳):筋骨格系のキネシオロジー 原著第3版. 医歯薬出版, 2020, pp22-26.
2)中村隆一, 齋藤宏, 長崎浩: 基礎運動学(第6版補訂). 医歯薬出版, 2013, pp40-42.
2021 年 8 月 30 日

コメント