肋間筋の作用（基礎運動学より）

はじめに

外肋間筋の作用は肋骨の挙上，内肋間筋の作用は肋骨の下制です。

筋の作用は，筋の起始，停止，走行を知っていれば，直感的に分かります。
例えば，上腕二頭筋が収縮すれば肘が曲がるということは明らかです。
しかし，肋間筋は分かりにくいのではないでしょうか？
この肋間筋の作用を，基礎運動学¹⁾では数式を使って説明していますが，この数式を読んでスッキリしたという人は稀でしょう。
そこで，まずは図を使って肋間筋の作用を説明してみたいと思います。
そのあと，数式についても解説します。

肋間筋の作用を図で確認

外肋間筋

基礎運動学¹⁾には以下のような図（図 1，一部改変）が載っています。

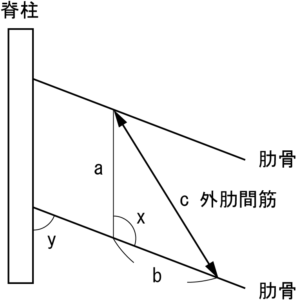
この図を動かしてみましょう。

まずは挙上です（図 2）。

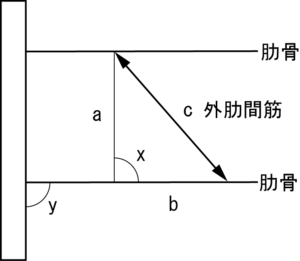
外肋間筋が短くなっています。
つまり外肋間筋が短縮すれば肋骨は挙上します。

次に下制です（図 3）。

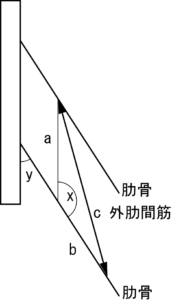
肋骨が下制すると外肋間筋は長くなります。
つまり，下制には作用しません。

内肋間筋

こちらも基礎運動学¹⁾の図を引用します（図 4，一部改変）。

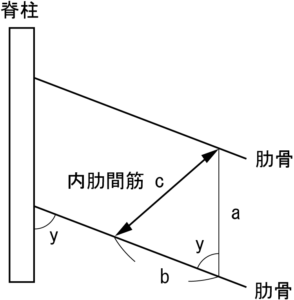
下制からみてみましょう（図 5）。

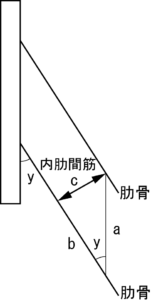
内肋間筋が短くなっていますので，下制に作用することが分かります。

次に挙上です（図 6）。

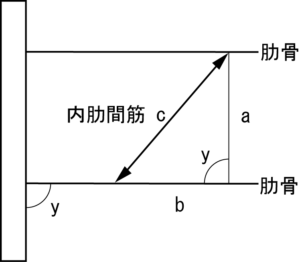
内肋間筋が長くなっていて，挙上には作用しないことが分かります。

数式について

「数式はパス！」とは割り切れない方のために，数式をざっくりと解説をしてみたいと思います（完璧な説明は数学に詳しい方に聞いてください^^;）。
高校数学が多少は分かるという方を想定して書きます。

まずは基礎運動学¹⁾にある解説を引用します。

外肋間筋の短縮が肋骨の挙上，内肋間筋の短縮が肋骨の引き下げに働くことを模式的に示す（図 7）。c と角 x の関係は，

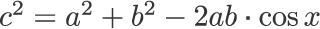
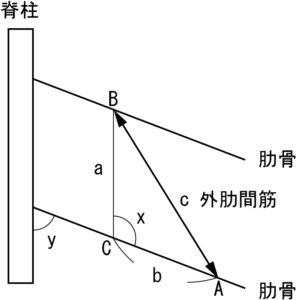
となり，肋骨と脊柱との角をy（x の補角）として x とおきかえると，

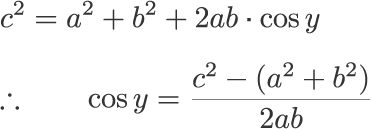
となります。

外肋間筋の方だけ解説します（内肋間筋も基本的な流れは一緒です）。

図 7は最初の図 1と同じですが，説明のために記号などを補足しています。

まず，三角形 ABC があることを確認してください。
そして，上の肋骨と下の肋骨は平行です。
上下の肋骨は同時に同じだけ動き，平行のままです。
脊柱と辺 a も平行のままで，辺 a，b の長さは変わりません。

式の大まかな方向性を示します。
最初の式は余弦定理です。
三角形の辺と角の関係を表す定理です。
角は三角比を使って間接的に表します。
今回の最初の式では，c の長さを，a と b の長さと角 x の大きさで表しています。
その式を変形すれば，辺 a，b，c の長さによって角xの大きさを表す式になります。
角xが分かると，平行であることに伴って角yの大きさが分かります。
その結果，辺 a，b の長さが変わらず，c が変化（外肋間筋が短縮）すれば角 y がどう変化するかが分かります。

今回の式では，先に x を y に置き換えています。
置き換えた結果が 2 番目の式です。
置き換えには以下の関係を使います。

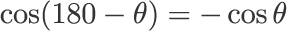
2 番目の式を変形したものが 3 番目の式で，y の角度と辺 a，b，c の関係を表しています。
3 番目の式より，c が小さくなれば cos y の値が小さくなります。
cos の値は，0 〜 90 度の間では，角度が大きくなるほど小さくなります。
つまり，cos y の値が小さくなると角 y は大きくなります。
よって，外肋間筋（c）が短くなれば，肋骨と脊柱の角度（y）が大きくなり，肋骨が挙上するということになります。

ややこしいことを書いてきましたが，三角形 ABC の c が短くなれば，角 x が小さくなるという，直感的には当たり前のことを数式で表現しているだけです。

さて，a と b は変わらず，c だけが変わるためには 2 本の肋骨が平行を保たなければならないのですが，2 本の肋骨が平行を保つ理由は示されていません。
片方の肋骨だけが動いたり，2 本の肋骨が動いて，互いに近づいていったりするかもしれません。
たぶん，2 本の肋骨のさらに上下の肋骨や肋間筋を考える必要があります。

ちなみに

余弦定理は別の定理に似ていますよね。

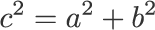
ピタゴラスの定理です。

ピタゴラスの定理は直角三角形で成り立つ定理で，それを一般の三角形に拡張したものが余弦定理です。
角度が大きくなりコサインの値が小さくなると，余弦定理の最後の項の値も小さくなります。
そして，90 度になると，cos 90° は 0 になって最後の項が消え，ピタゴラスの定理が出現します。
この関係に美しさを感じる人は数学に向いています。
美しさを感じない人は，今回取り上げた肋間筋の作用を表す数式には取り組まない方がいいのかもしれません。

こちらの記事もおすすめ

呼吸筋の一覧

参考文献

1）中村隆一, 齋藤宏, 長崎浩: 基礎運動学（第6版補訂）. 医歯薬出版, 2013, pp288-289.

2019 年 11 月 7 日
2020 年 4 月 25 日