物理療法における逆 2 乗の法則

はじめに

赤外線療法，極超短波療法などの電磁波を用いた物理療法における，照射距離とエネルギーの強さに関する法則である，逆 2 乗の法則（inverse square law）について解説します。

数学的，物理学的にある程度正しく理解することを目指しています。

「電磁波」だとイメージしにくいかもしれませんので，ここからは「光」を例として説明します。

逆 2 乗の法則とは，「光のエネルギーの強さは光源からの距離の 2 乗に反比例する」という法則です。

距離の 2 乗の逆数に比例するともいえます。

例えば，距離が 2 倍になればエネルギーの強さは 1 / 4 になり，距離が 1 / 2 になればエネルギーの強さは 4 倍になります。

ここでいうエネルギーの強さとは，単位面積あたりのエネルギーの量です。

法則が成り立つためには，光が全方向に偏りなく放射され，まっすぐ進むという条件が必要です。

エネルギーとは何かということは，ここではあまり深く考えないほうがいいでしょう。
エネルギー量が多ければ，より暖まるくらいでいいと思います。

逆自乗の法則¹⁾，あるいは距離逆比例の法則²⁾とも呼ばれます。

距離が増えればエネルギーが弱くなることを図 1 で説明します。

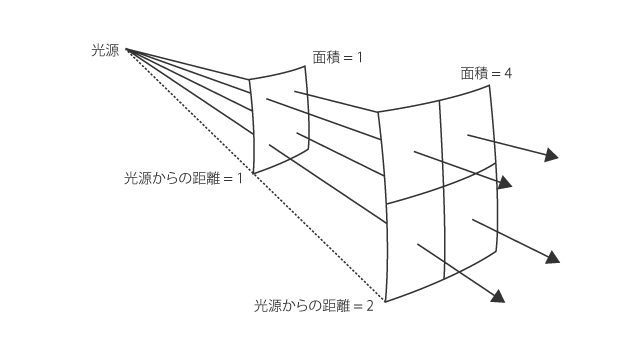
矢印は光が進む方向であり，矢印はそれぞれ同じ量のエネルギーをもっています。
エネルギーの強さとは単位面積あたりのエネルギーの量のことでしたので，同じ面積の領域を何本の矢印が通過するかで，エネルギーの強さを表現することができます。

図 1 には 4 本の矢印が描かれており，この 4 本の光に注目して考えていきます。

光源に近い側に四角形の領域があります（球面上の四角形です^注)）。
そこを 4 本の矢印が通っています。
仮に，四角形の面積が 1 で，矢印 1 本のエネルギーが 1 であるとするなら，この四角形を通るときの光のエネルギーの強さは 4 です。

光は放射状に広がりながら進んでいきますので，光源から遠くなるほど，より広い領域を進むことになります。

光源から遠い方の四角形の領域は，4 つに区切られていて，区切られた部分の面積は，光源に近い側の四角形の面積と同じです。
つまり，遠い方の面積は 4 です。
光源からの距離は 2 倍です。

光源から遠い方の領域を通過するとき，全体としては 4 本の矢印が通っていますが，近い方と同じ面積の部分だけをみれば，矢印は 1 本しか通っていません。
ですので，単位面積あたりのエネルギー量であるエネルギーの強さは 1 ということになります。

近い方の四角形を通るときのエネルギーの強さは 4 でしたが，2 倍の距離にある遠い方の四角形を通るときには 1 になっていて，1 / 4 に減っています。

以上が逆 2 乗の法則のイメージになります。

次は，ちゃんと計算してみましょう。

距離の 2 乗に反比例することを，数字で示したいと思います。

球の中心に光源があるとします。
そこから全方向に均等に光が出ていきます。
光源から出る全ての光のエネルギーの合計は E だとします。
このエネルギーの総量 E は，光源からどれだけ離れても変わりません。
減るのは単位面積あたりのエネルギー量です。

距離 r だけ進んだところでのエネルギーの強さを計算してみましょう。

全方向に向かって同じスピードで進むのですから，距離 r だけ進んだところでの，光が分布する面は球になり，その面積は，半径 r の球の表面積になります。
そして，エネルギーの強さとは単位面積あたりのエネルギーの量ですので，エネルギーの総量 E を半径 r の球の表面積で割ることになります。

分母に r² がありますので，エネルギーの強さは光源からの距離の 2 乗に反比例することが分かります。

次に，2 倍の距離 2r 進んだところでのエネルギーの強さも計算しておきましょう。
計算の仕方は，距離 r だけ進んだときと同じです。

式を変形していくと，距離 2r でのエネルギーの強さは，距離 r でのエネルギーの強さに 1 / 4 をかけた値になることを示す式になります。

逆 2 乗の法則が成り立つためには，電磁波が全方向に偏りなく放射される必要があります。
実際の物理療法機器が電磁波を全方向に偏りなく放射しているのかどうかは分かりませんでした。

図 1 の四角形は，前述の計算の方法から考えると，球面上の四角形でなければなりません。
教科書等で，平面で描かれていることがありますが，それだと，四角形内の位置によって光源からの距離が変わってしまいますので，あまり正確な図ではありません。
間違いではないでしょうが，，，

1）岩田由明: 光線療法, 理学療法ハンドブック改訂第4版第2巻. 細田多穂, 柳澤健（編）, 協同医書出版社, 2010, pp759-779.
2）嶋田智明, 田口順子, 他: 物理療法マニュアル. 医歯薬出版, 1998, pp87.

2021 年 7 月 12 日